クロスシミュレーション用平面ポリゴンの作成方法
ドロネー分割とは、平面上に置かれた任意の位置の点を結んで三角形の集合を作る手法です。
この手法を使って、任意の閉じた平面形状をポリゴン化する方法を解説します。
目的と結果
二次元CADで作った服のパターンをドロネー分割で小さな三角形の集合体に置き換え、三次元空間に持って行って、縫い合わせ、3D人体データに着せることが目的です。
結果こんな感じで、三次元CAD化することができました。
単純にパターン楽天 を分割するだけではなく、再分割して三角形の大きさを変えて計算速度と外見の釣り合いを調整したり、格子の向きを変えて、布地のバイアス効果を表現できるようにもなりました。
ドロネー分割による三角形の作り方
まずは全ての点を含む大きな三角形を作ります。
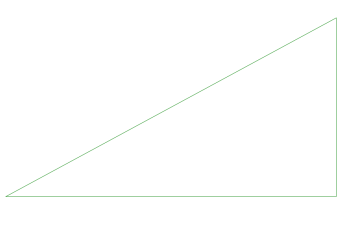
点を三角形の上におきます。
最初の大きな三角形は全ての点を含んでいるので、プロットした点は必ず三角形の中に入ります。
点を使って三角形を三つに分割します。
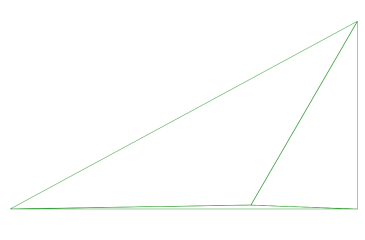
順番に点を置いてゆき、点が含まれる三角形を三つに分割する作業を続けます。
単純に分割するだけだと妙に細長い三角形ができてしまうので、フリップという作業を行い、三角形をなるべく正方形に近くします。
フリップが必要か調べる三角形の三点を通る円を描き、この中に、隣の三角形の残り一つの頂点が含まれているかどうかを確認します。
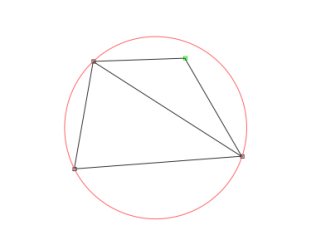
含まれていたら、この二つの三角形をまとめて四角にして、別の頂点を使って新たな三角形に組み替えます。
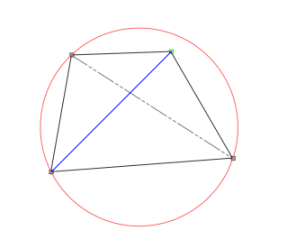
フリップを繰り返すことで、三角形の形状が最適化されます。
クロスシミュレーション
製図した服のパターンを3次元空間に持って行き、曲げられるようにしたいので、分割を行いました。
単純に任意の形状の平面を三次元に持って行っても曲げることができません。小さな三角形(ポリゴン)に分割すれば、これが可能になります。
製図した服を、三次元空間で縫い合わせ、3Dスキャナーで取り込んだ人の3Dデータに着せることができるようにする予定です。
任意形状の分割の方法
まずパターン外形線を点の集合に置き換えます。
この点が全て入る大きな三角形を描き、外形線の構成する点を順番において三角形を分割して行きます。

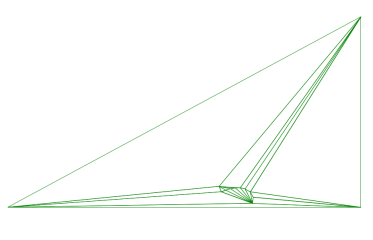
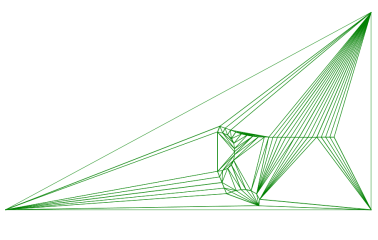
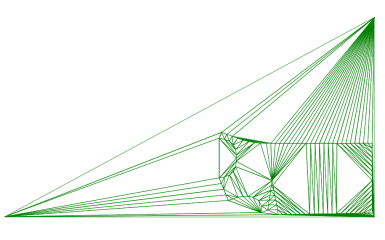
全ての外形点を置いて分割し終えたら、外径の外側にある三角形を全て消去します。
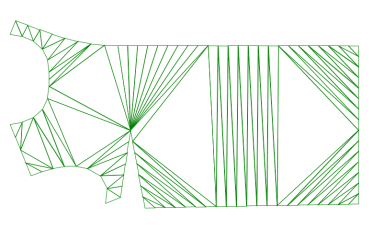
この後形状の内部に一定の間隔で点を置いて行き、さらに分割を進めます。
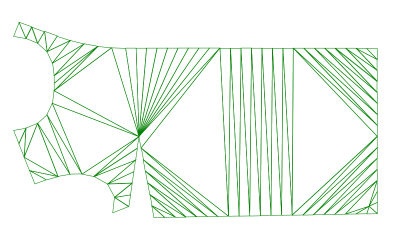
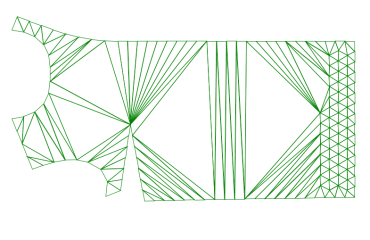
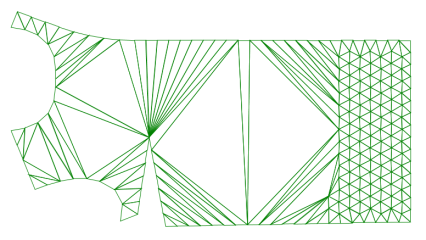
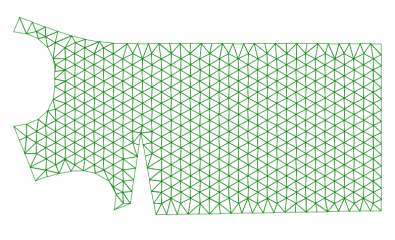
これでパターンのポリゴン化が完成します。
最初に外形点を置き、外形の外にある三角形を消去してから内部の点を置くのがコツです。外部三角形を消さないと外形が崩れてしまいます。
外形点間隔はある程度小さくしておきます。大きすぎると外形が崩れる原因になります。
直線の分割
基本的に分割点は三角形の中にありますが、既存の点と重なっていたり、三角形の境界上にある場合があります。
直線状に並んだ点を分割する場合、追加する点が三角形の境界上にあるケースが発生します。
この場合は境界を持つ三角形を2つに分割します。
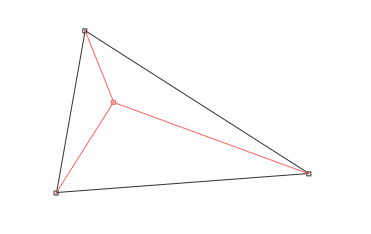
通常は3つに分割する
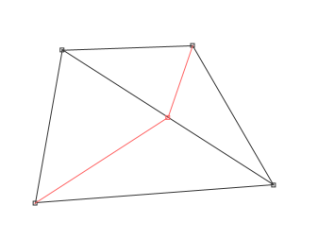
線上の場合は、線を持つ3角形を二つに分割
ネットで検索したドロネー分割方法ではこの線上のケースがなかったので、高さ0の三角形ができてしまい、原因を探るのに苦労しました。
穴がある場合
パターンの中にダーツがある場合はこの部分を穴にします。
ダーツ線を点の集合にして、外形点の前、最初に配置します。
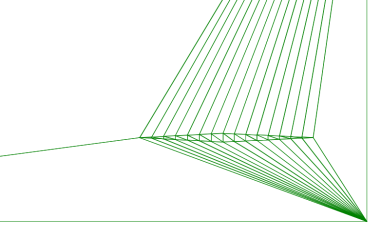
配置を終えたら、穴の中にある三角形を削除します。
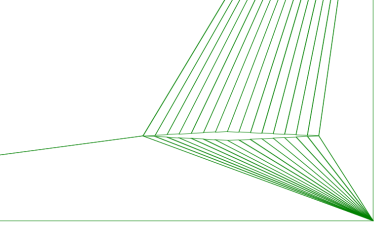
この後外形点を配置していけば、穴の空いたパターンが作れます
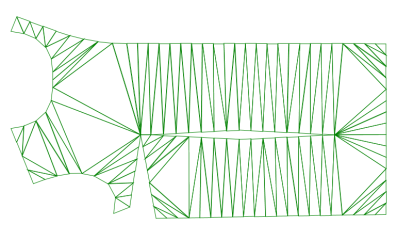

三角形の大きさ
構成する三角形(ポリゴン)は小さいほど滑らかに曲げられるので実際の布に近くなります。
しかし、小さくなるほど計算量が増大するので、過剰に小さくすると大変な時間がかかるようになります。
点をバネでつなぐ
最後に作った三角形の辺をバネでつなぎます。

布の縦糸横糸方向には伸びにくく、バイアス方向は伸びやすいようにばね定数を決めてあげると布らしい乗り方が再現できます
となりの三角形の反対側の頂点にもバネを設定してつなぎます。これは布のしなやかさを表現するためのものです。
バネを強くすると張りのある布、弱くするとフニャフニャの布になります。
意外な落とし穴
こうしてパターン三角形に分割することができるようになりましたが、時々分割がおかしくなるケースがありました。
正三角形の集合体で構成すると出ないのですが、直角二等辺三角形で構成するとおかしくなってしまいます。
布目の方向と分割を一致させたいので、どうしても直角二等辺三角形にしたいのです。
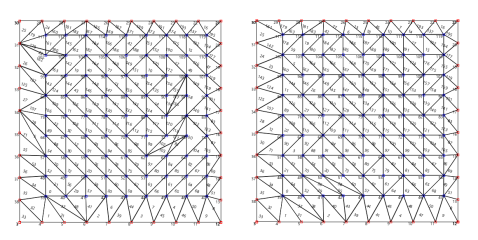
このバグをなかなか見つけられなかったのですが、3点円を描くときにある条件で円がおかしくなってしまうことがわかりました。
3点円弧を描くメソッドに直角二等辺三角形を描くと生ずるバグがあったのです。
これを修正したところ、うまく動くようになりました。
最終更新日: 2020-05-17 11:09:32