クロス(布)シミュレーションのサンプルプログラム
布のシミュレーションに使う四角い布のサンプルプログラムを紹介します。
JavaFXで下のように動きます。

Class一覧
このサンプルプログラムで使うClassは下記の通り
NunoMesh.java 布を表す
Point.java 布を構成する点
NTriangle.java 布を構成する三角形
Spring.java 構成点を結ぶバネ
ThreeDimension.java 3次元座標またはベクトルを格納
ThreeDExe.java 3次元座標を計算
NunoAnimation.java シミュレーション実行
布の構造
点とバネと三角形で構成します。
点には質量を付け、重力など様々な力をここに加えます。
バネは点同士をつなぎとめるためのものです。
三角形は三つの点で構成され、面を形成します。
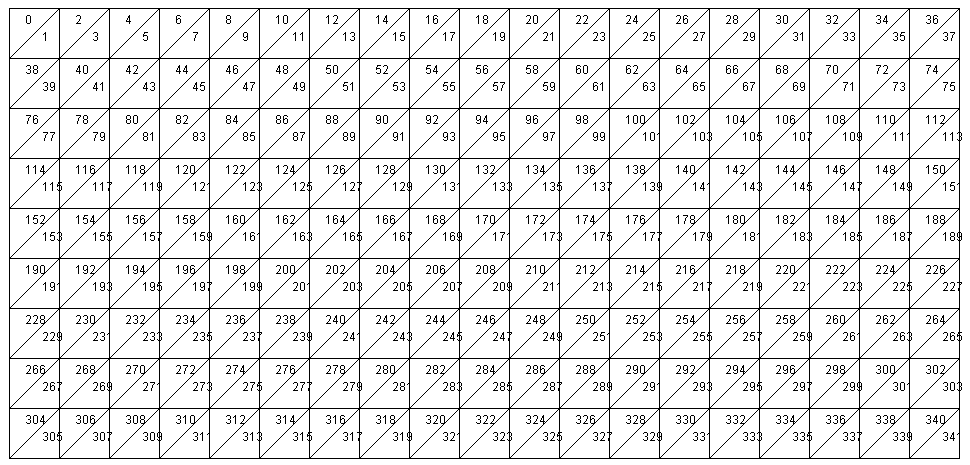
x方向20、y方向に10の点で構成される布を例にして、順に説明してゆきます
点
20×10個の点を用意します。xy平面に並べると、こんな感じ。

点のclassは下記。点の座標、周りの点と常がる8本のバネ、点の重量、点にかかる力のベクトル、配列番号を格納します。
package tomojavalib.nuno;
/**布を構成する点のclass*/
public class Point {
//座標
public ThreeDimension d = null;
//隣接点を結ぶバネ
public Spring[] sp = new Spring[8];
//重量
public double m = 1.;
//点にかかる力
ThreeDimension f = null;
//配列番号を格納
public int pn=0;
/**コンストラクタ*/
public Point( ThreeDimension td ,int pn ){
d = new ThreeDimension( td.x ,td.y , td.z);
f = new ThreeDimension(0.,0.,0.);
for(int i=0;i<sp.length;i++){ sp[i] = null; }
this.pn = pn;
return;
}
}
布のCalss、NunoMesh.javaのコンストラクタで、点pを下記のように初期化します。
stx,styは点の最初の座標、px,pyは点間ピッチです。
int nos = (int)(x*y);
p = new Point[ nos ];
//点を作成
int n =0;
for(int ii=0;ii<y;ii++){
for(int i=0;i<x;i++){
double ax = stx + px*i ;
double ay = sty + py*ii ;
p[n] = new Point( new ThreeDimension( ax , ay , 0. ),n);
n++;
}
}
バネ
構成点を結びます。下図のように結びます。
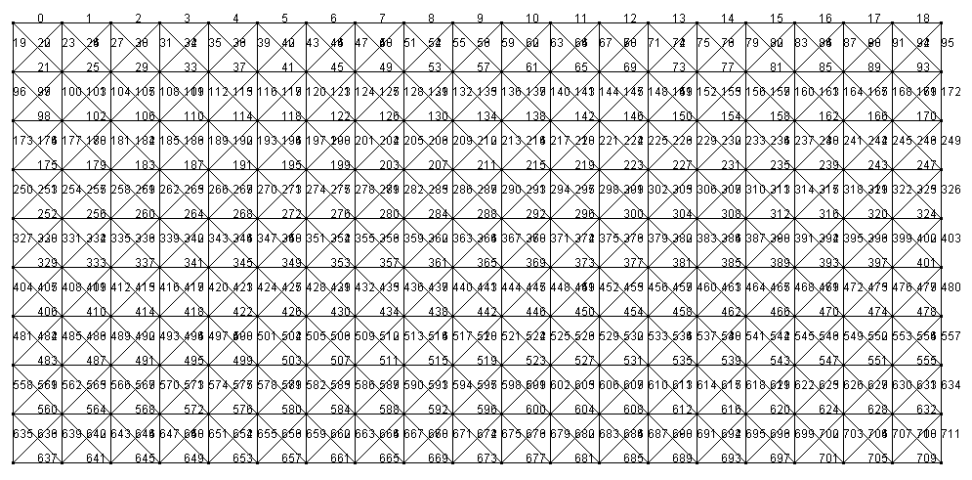
バネのClassは下記。
結ぶ2点、初期長さ、初期ベクトル、配列番号を格納します。
メソッドとして、バネ定数を決めるsetSpringConstant()、単位ベクトルを返すgetV()を持ちます。
package tomojavalib.nuno;
/**布を構成する点と点を結ぶバネ要素*/
public class Spring {
Point[] p = new Point[2];
//初期長さ
double l=0.;
//初期ベクトル
ThreeDimension sv ;
//バネ定数
double k = 0.1;
ThreeDExe e=null;
//番号
int sn =0;
public Spring( Point sp,Point ep, int sn ){
e = new ThreeDExe();
p[0]=sp;
p[1]=ep;
l = e.getLen( p[0].d , p[1].d );
sv = e.setLen( e.minus(p[0].d, p[1].d) , 1. );
k = this.setSpringConstant( sv );
this.sn = sn;
}
/**バネ係数の設定*/
private double setSpringConstant( ThreeDimension ssv ){
double sc =0.;
if(ssv.x>=0.){if(ssv.y>=0.){sc = Math.sqrt( ssv.x*ssv.x +(1-ssv.x)*(1-ssv.x) );}}
if(ssv.x<=0.){if(ssv.y>=0.){sc = Math.sqrt( ssv.x*ssv.x +(1+ssv.x)*(1+ssv.x) );}}
if(ssv.x<=0.){if(ssv.y<=0.){sc = Math.sqrt( ssv.x*ssv.x +(-1-ssv.x)*(-1-ssv.x) );}}
if(ssv.x>=0.){if(ssv.y<=0.){sc = Math.sqrt( ssv.x*ssv.x +(ssv.x-1)*(ssv.x-1) );}}
sc = sc *1.2;
return sc;
}
//現在の単位ベクトルを返す
public ThreeDimension getV(){
ThreeDimension rd = e.setLen( e.minus(p[0].d, p[1].d) , 1. );
return rd;
}
}
布は縦横方向に伸びにくく、斜め方向には伸びやすい性質があります。setSpringConstant()でバネの方向からバネ定数を決めています。
布のCalss、NunoMesh.javaのコンストラクタで、バネspを下記のように初期化します。
バネ配列の数nは、構成点がx×y個とすると、
n = (x-1)*(y-1)*2 + (x-1)*y + x*(y-1);
n個のバネをそれぞれをつなぐ点を入れて初期化します。
各点には8つのバネが繋がるので、このうちの4つをシャローコピー(shallow copy)で点の中に格納します。
sp = new Spring[n];
int pn=0; int sn=0;
for(int iy=0;iy<y;iy++){
for(int ix=0;ix<x;ix++){
//ばね0
if(ix!=0){if(iy!=0){ sp[sn] = new Spring(p[pn], p[ x * (iy-1) + (ix-1) ],sn); p[pn].sp[0] = sp[sn]; sn++; }}
//ばね1
if(iy!=0){sp[sn] = new Spring(p[pn], p[ x * (iy-1) + (ix) ],sn); p[pn].sp[1] = sp[sn]; sn++; }
//ばね2
if(ix!=x-1){if(iy!=0){ sp[sn] = new Spring(p[pn], p[ x * (iy-1) + (ix+1) ],sn); p[pn].sp[2] = sp[sn]; sn++; }}
//ばね3
if(ix!=x-1){ sp[sn] = new Spring(p[pn], p[ x * (iy) + (ix+1) ],sn); p[pn].sp[3] = sp[sn]; sn++; }
pn++;
}}
あとから残りの4つも点に格納
//点を結ぶばねを生成(下半分)
pn=0;
for(int iy=0;iy<y;iy++){
for(int ix=0;ix<x;ix++){
//ばね4
if(ix!=x-1){if(iy!=y-1){
int s = p[ x * (iy+1) + (ix+1) ].sp[0].sn;
p[pn].sp[4] = sp[s];
}}
//ばね5
if(iy!=y-1){
int s = p[ x * (iy+1) + (ix) ].sp[1].sn;
p[pn].sp[5] = sp[s];
}
//ばね6
if(ix!=0){if(iy!=y-1){
int s = p[ x * (iy+1) + (ix-1) ].sp[2].sn;
p[pn].sp[6] = sp[s];
}}
//ばね7
if(ix!=0){
int s = p[ x * (iy) + (ix-1) ].sp[3].sn;
p[pn].sp[7] = sp[s];
}
pn++;
}}
これでバネの初期化終了。例えば、点[50]のもつバネsp[]0~7を見ると、下記のような繋がりになります。
端の方の点にはバネが8つありませんが、ない部分はnullのままにしておき、計算時nullであればとばすようにしています。
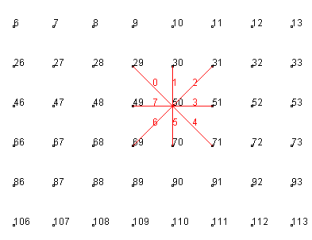
三角形
3つの点を結んで、布を隙間なく覆います。
三角形のclassは下記。
構成する3つの点と、自らの配列番号を格納。
package tomojavalib.nuno;
/**布を構成する三角形のclass*/
public class NTriangle {
//構成する3点
Point[] p = new Point[3];
//配列番号
public int tn;
public NTriangle( Point p1 , Point p2 , Point p3 ,int tn){
p[0]=p1; p[1]=p2;p[2]=p3;
this.tn= tn;
}
}
布のCalss、NunoMesh.javaのコンストラクタで、三角形tを下記のように初期化します。
三角形の配列の数nosは、構成点がx×y個とすると、
nos =(int)(x-1)*(y-1)*2;
t = new NTriangle[ nos ];
それぞれの三角形に点をシャローコピーで格納します。
三角形で面を表しますが、点の取り方で裏表が決まるので、すべての三角形の裏表が同じになるようにします。
//三角形を生成
n =0;
for(int ii=0;ii<y-1;ii++){
for(int i=0;i<x-1;i++){
int p1 = x*ii+i;
int p3 = p1+1;
int p2 = x*(ii+1)+i;
t[n] = new NTriangle( p[p1] , p[p2] , p[p3] ,n);
n++;
p1 = x*ii+i+1;
p2 = x*(ii+1)+i;
p3 = p2+1;
t[n] = new NTriangle( p[p1] , p[p2] , p[p3] ,n);
n++;
}
}
布
布を示すClass、NunoMeshは以下の通り。
makeNewSheet()で構成する点、バネ、三角形を初期化します。
move()は布を構成する点にかかる力を計算します。
布は重力で下に引っ張られますが、固定している点があるため下には落ちません。そのため、各点の間のバネで引っ張り合いになり、釣り合うところまで移動します。
addGF()が重力、addSpF()がバネの力を点に加えます。fixPoint()は固定点の位置を一定に保ちます。
cleateTriangleMesh()は表示に必要なTriangleMeshを作成。
計算後の各点の位置データはgetPoints()で取り出し、JavaFX楽天 にて表示されているTriangleMeshに渡すことで動きを表示します。
package tomojavalib.nuno;
import javafx.scene.shape.TriangleMesh;
public class NunoMesh {
//三角形
public NTriangle[] t = null;
//点
public Point[] p = null;
//ばね
public Spring[] sp = null;
//計算class
ThreeDExe e=null;
//固定点
private Point[] fixpoint = null;
/**
* 新規四角形のメッシュを作成します
* @param px x方向のピッチ
* @param py y方向のピッチ
* @param stx はじめるx座標
* @param sty はじめるy座標
* @param x x方向の数
* @param y y方向の数
*/
public void makeNewSheet(double px,double py,double stx,double sty,int x,int y ){
e = new ThreeDExe();
//点と3角形の準備
int nos = (int)(x*y);
p = new Point[ nos ];
nos =(int)(x-1)*(y-1)*2;
t = new NTriangle[ nos ];
//点を作成
int n =0;
for(int ii=0;ii<y;ii++){
for(int i=0;i<x;i++){
double ax = stx + px*i ;
double ay = sty + py*ii ;
p[n] = new Point( new ThreeDimension( ax , ay , 0. ),n);
n++;
}
}
//三角形を生成
n =0;
for(int ii=0;ii<y-1;ii++){
for(int i=0;i<x-1;i++){
int p1 = x*ii+i;
int p3 = p1+1;
int p2 = x*(ii+1)+i;
t[n] = new NTriangle( p[p1] , p[p2] , p[p3] ,n);
n++;
p1 = x*ii+i+1;
p2 = x*(ii+1)+i;
p3 = p2+1;
t[n] = new NTriangle( p[p1] , p[p2] , p[p3] ,n);
n++;
}
}
//点を結ぶばねを生成(上半分)
n = (x-1)*(y-1)*2 + (x-1)*y + x*(y-1);
sp = new Spring[n];
int pn=0; int sn=0;
for(int iy=0;iy<y;iy++){
for(int ix=0;ix<x;ix++){
//ばね0
if(ix!=0){if(iy!=0){ sp[sn] = new Spring(p[pn], p[ x * (iy-1) + (ix-1) ],sn); p[pn].sp[0] = sp[sn]; sn++; }}
//ばね1
if(iy!=0){sp[sn] = new Spring(p[pn], p[ x * (iy-1) + (ix) ],sn); p[pn].sp[1] = sp[sn]; sn++; }
//ばね2
if(ix!=x-1){if(iy!=0){ sp[sn] = new Spring(p[pn], p[ x * (iy-1) + (ix+1) ],sn); p[pn].sp[2] = sp[sn]; sn++; }}
//ばね3
if(ix!=x-1){ sp[sn] = new Spring(p[pn], p[ x * (iy) + (ix+1) ],sn); p[pn].sp[3] = sp[sn]; sn++; }
pn++;
}}
//点を結ぶばねを生成(下半分)
pn=0;
for(int iy=0;iy<y;iy++){
for(int ix=0;ix<x;ix++){
//ばね4
if(ix!=x-1){if(iy!=y-1){
//p[pn].sp[4] = p[ x * (iy+1) + (ix+1) ].sp[0];
int s = p[ x * (iy+1) + (ix+1) ].sp[0].sn;
p[pn].sp[4] = sp[s];
}}
//ばね5
if(iy!=y-1){
//p[pn].sp[5] = p[ x * (iy+1) + (ix) ].sp[1];
int s = p[ x * (iy+1) + (ix) ].sp[1].sn;
p[pn].sp[5] = sp[s];
}
//ばね6
if(ix!=0){if(iy!=y-1){
//p[pn].sp[6] = p[ x * (iy+1) + (ix-1) ].sp[2];
int s = p[ x * (iy+1) + (ix-1) ].sp[2].sn;
p[pn].sp[6] = sp[s];
}}
//ばね7
if(ix!=0){
//p[pn].sp[7] = p[ x * (iy) + (ix-1) ].sp[3];
int s = p[ x * (iy) + (ix-1) ].sp[3].sn;
p[pn].sp[7] = sp[s];
}
pn++;
}}
return;
}
/**FX用のTriangleMeshを作成*/
public TriangleMesh cleateTriangleMesh()
{
// メッシュ
TriangleMesh tmesh = new TriangleMesh();
// 点を作成
float[] points = new float[ t.length * 9 ];
int pi=0;
for(int i=0;i<this.t.length;i++){
for(int ii=0;ii<3;ii++){
points[pi] =(float)this.t[i].p[ii].d.x; pi++;
points[pi] =(float)this.t[i].p[ii].d.y; pi++;
points[pi] =(float)this.t[i].p[ii].d.z; pi++;
}}
//coords作成
float[] texCoords = new float[ t.length * 6 ];
int ti=0;
for(int i=0;i<this.t.length;i++){
for(int ii=0;ii<3;ii++){
texCoords[ti] =(float)(this.t[i].p[ii].d.x );
ti++;
texCoords[ti] =(float)(this.t[i].p[ii].d.y );
ti++;
}
}
//face作成
int[] faces = new int[ (int)(points.length/3.*2) ];
int fi=0;
for(int i=0;i<faces.length/2.;i++){
faces[fi] = i; fi++;
faces[fi] = i; fi++;
}
tmesh.getPoints().addAll( points );
tmesh.getTexCoords().addAll( texCoords );
tmesh.getFaces().addAll( faces );
return tmesh;
}
/**服に動きを与える*/
public void move(){
//速度初期化
resetF();
//ばねによる力を加える
this.addSpF();
//重力を加える
this.addGF();
//位置を更新
movePoint();
//固定点を修正
fixPoint();
return;
}
//固定点をセット
public void setFixPoint( int[] no){
fixpoint = new Point[no.length];
for(int i=0;i<fixpoint.length;i++){
fixpoint[i] = new Point( new ThreeDimension( p[no[i]].d.x , p[no[i]].d.y , p[no[i]].d.z+5 ) , p[no[i]].pn );
}
}
int ii=0;
//固定点の位置固定
private void fixPoint(){
for(int i=0;i<fixpoint.length;i++){
ii++;
System.out.println(p[ fixpoint[i].pn ].d.x);
if(ii<500){if( p[ fixpoint[i].pn ].d.x >-50){
fixpoint[i].d.x = fixpoint[i].d.x-.1;
if (i % 2 == 0){
fixpoint[i].d.z = fixpoint[i].d.z-.1;
}else{
fixpoint[i].d.z = fixpoint[i].d.z+.1;
}
}}
p[ fixpoint[i].pn ].d.x = fixpoint[i].d.x ;
p[ fixpoint[i].pn ].d.y = fixpoint[i].d.y ;
p[ fixpoint[i].pn ].d.z = fixpoint[i].d.z ;
}
}
/**スプリングの力を加える*/
private void addSpF(){
//スプリングの力を計算
for(int pi=0;pi<p.length;pi++){
//点にかかる力
//ThreeDimension pf = new ThreeDimension(0.,0.,0.);
//点にかかる加速度
//ThreeDimension pa = new ThreeDimension(0.,0.,0.);
//各スプリング
for(int si=0;si<p[pi].sp.length;si++){
if(p[pi].sp[si]!=null){if(p[pi].sp[si].pflug){
//スプリング長さを計算
double sl = e.getLen( p[pi].sp[si].p[0].d , p[pi].sp[si].p[1].d );
//伸び量
double dl = sl - p[pi].sp[si].l ;
//力を計算
double k = p[pi].sp[si].k*-1;
//引張には強く、縮みには弱い反力
//if(dl<0.){ k= k*0.1; }
//スプリングの番号で方向を変換
if(si>3){ k = k * (-1.); }
ThreeDimension sf = e.kakeru(p[pi].sp[si].getV(), dl * k );
p[pi].f = e.plus(p[pi].f,sf);
}}
}}
}
/**服に重力の力を加える*/
private void addGF(){
ThreeDimension g = new ThreeDimension(0.,-.6,0.);
//スプリングの力を計算
for(int pi=0;pi<p.length;pi++){
//速度を更新
p[pi].f = e.plus( p[pi].f , g );
}
}
/**個々の点を移動させる*/
private void movePoint(){
//位置を更新
for(int pi=0;pi<p.length;pi++){
//速度の減衰
p[pi].f = e.kakeru( p[pi].f , .2 );
ThreeDimension d = e.plus( p[pi].d , p[pi].f );
p[pi].d.x = d.x;p[pi].d.y = d.y;p[pi].d.z = d.z;
}
}
/**個々の点を移動させる*/
private void resetF(){
//位置を更新
for(int pi=0;pi<p.length;pi++){
p[pi].f.x=0.;p[pi].f.y=0.;p[pi].f.z=0.;
}
}
/**TriangleMeshに渡すための点座標配列を返す*/
public float[] getTPoints(){
// 点を作成
float[] points = new float[ t.length * 9 ];
int pi=0;
for(int i=0;i<this.t.length;i++){
for(int ii=0;ii<3;ii++){
points[pi] =(float)this.t[i].p[ii].d.x; pi++;
points[pi] =(float)this.t[i].p[ii].d.y; pi++;
points[pi] =(float)this.t[i].p[ii].d.z; pi++;
}}
return points;
}
}
アニメーション
クロス(布)シミュレーションを表示するclassです。
カメラ、照明など、表示に必要なノードを用意して、布を作り、動かします。
Java
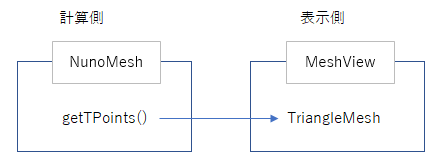
楽天 FXでメッシュ表示に使うMeshViewとここで作ったNunoMeshの関係は、
まずMeshViewに必要なTriangleMeshをNunoMeshで生成してMeshViewに渡す。
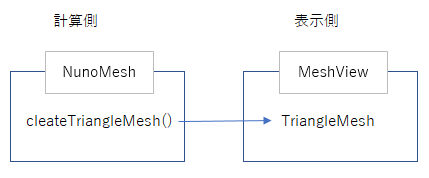
そのあと、アニメーションのループ内で計算、移動した点の位置情報をNunoMeshから取り出してMeshViewにわたします。
package tomojavalib.nuno;
import javafx.animation.AnimationTimer;
import javafx.application.Application;
import javafx.geometry.*;
import javafx.scene.*;
import javafx.scene.paint.Color;
import javafx.scene.shape.*;
import javafx.scene.transform.*;
import javafx.stage.Stage;
/**布アニメーション*/
public class NunoAnimation extends Application {
NunoMesh nuno = null;
TriangleMesh t = null;
public static void main(String[] args) {
Application.launch(args);
}
@Override
public void start(Stage stage) throws Exception {
Group group = new Group();
Scene scene = make3dScene( group );
stage.setScene(scene);
this.addNuno( group );
//タイトルの表示
stage.setTitle("布アニメーション試験");
stage.show();
//アニメーションを始める
new Animation().start();
}
private void addNuno( Group group ){
nuno = new NunoMesh();
nuno.makeNewSheet(5, 5, -50, -50, 20, 10);
int[] no = new int[]{180,185,190,195,199};
nuno.setFixPoint( no );
t = nuno.cleateTriangleMesh();
MeshView meshView = new MeshView();
meshView.setMesh( t );
meshView.setCullFace(CullFace.NONE);
group.getChildren().add( meshView );
}
private Scene make3dScene( Group group ){
//
カメラ
楽天 を置く
PerspectiveCamera camera = new PerspectiveCamera( true );
Translate cameratranslate = new Translate(0,30,-500);
Rotate camerarotateX = new Rotate( 180 , new Point3D( 1 , 0 , 0 ) );
Rotate camerarotateY = new Rotate( 30 , new Point3D( 0 , 1 , 0 ) );
camera.getTransforms().add( camerarotateX );
camera.getTransforms().add( camerarotateY );
camera.getTransforms().add( cameratranslate );
camera.setFarClip( 5000. );
camera.setFieldOfView( 15. );
group.getChildren().add( camera );
//点光源を置く
LightBase light = new PointLight();
light.setTranslateY( -100.0 );
light.setTranslateZ( -100.0 );
light.setTranslateX( -000.0 );
group.getChildren().add( light );
//Sceneの設定
Scene s3d = new Scene(group, 640, 480,true, SceneAntialiasing.BALANCED);
s3d.setFill(Color.BLUE);
s3d.setCamera( camera );
return s3d;
}
private class Animation extends AnimationTimer {
int a=0;
@Override
public void handle(long now) {
a++;
System.out.println(a);
//布を動かす
nuno.move();
//動いたのちの点を取り出す
float[] newPoints = nuno.getTPoints();
// 計算後の位置情報を渡す
t.getPoints().setAll( newPoints );
}
}
}
3次元座標関係
3次元座標やベクトル計算が必要なので、これをまとめておきました。
3次元座標やベクトルを格納するclass、ThreeDimension
単純に3つの数値を格納します。
public class ThreeDimension {
public double x;
public double y;
public double z;
public ThreeDimension( double tx , double ty , double tz ){x =tx;y=ty;z=tz;}
public ThreeDimension(){x =0.;y=0.;z=0.;}
}
座標、ベクトルの計算。
足し算、掛け算など簡単にできるように用意しました。他に内積とか外積のメソッドもあると便利。
package tomojavalib.nuno;
/**3次元座標の計算*/
public class ThreeDExe {
/**足し算*/
public ThreeDimension plus( ThreeDimension t1 , ThreeDimension t2 ){
ThreeDimension rt = new ThreeDimension();
rt.x = t1.x + t2.x;
rt.y = t1.y + t2.y;
rt.z = t1.z + t2.z;
return rt;
}
/**足し算*/
public ThreeDimension plus( ThreeDimension t1 , double m ){
ThreeDimension rt = new ThreeDimension();
rt.x = t1.x + m;
rt.y = t1.y + m;
rt.z = t1.z + m;
return rt;
}
/**引き算*/
public ThreeDimension minus( ThreeDimension t1 , ThreeDimension t2 ){
ThreeDimension rt = new ThreeDimension();
rt.x = t1.x - t2.x;
rt.y = t1.y - t2.y;
rt.z = t1.z - t2.z;
return rt;
}
/**引き算*/
public ThreeDimension minus( ThreeDimension t1 , double m ){
ThreeDimension rt = new ThreeDimension();
rt.x = t1.x - m;
rt.y = t1.y - m;
rt.z = t1.z - m;
return rt;
}
/**掛け算*/
public ThreeDimension kakeru( ThreeDimension t1 , ThreeDimension t2 ){
ThreeDimension rt = new ThreeDimension();
rt.x = t1.x * t2.x;
rt.y = t1.y * t2.y;
rt.z = t1.z * t2.z;
return rt;
}
/**掛け算*/
public ThreeDimension kakeru( ThreeDimension t1 , double m ){
ThreeDimension rt = new ThreeDimension();
rt.x = t1.x * m;
rt.y = t1.y * m;
rt.z = t1.z * m;
return rt;
}
/**割り算*/
public ThreeDimension waru( ThreeDimension t1 , ThreeDimension t2 ){
if( t2.x==0.){ return null; }if( t2.y==0.){ return null; }if( t2.z==0.){ return null; }
ThreeDimension rt = new ThreeDimension();
rt.x = t1.x / t2.x;
rt.y = t1.y / t2.y;
rt.z = t1.z / t2.z;
return rt;
}
/**割り算*/
public ThreeDimension waru( ThreeDimension t1 , double m ){
if( m==0.){ return null; }
ThreeDimension rt = new ThreeDimension();
rt.x = t1.x / m;
rt.y = t1.y / m;
rt.z = t1.z / m;
return rt;
}
/**長さを返す*/
public double getLen( ThreeDimension t1 ){
double l = Math.sqrt( t1.x*t1.x + t1.y*t1.y + t1.z*t1.z );
return l;
}
/**座標間距離を返す*/
public double getLen( ThreeDimension t1 ,ThreeDimension t2 ){
double l = Math.sqrt( (t1.x - t2.x )*(t1.x - t2.x ) + (t1.y - t2.y )*(t1.y - t2.y ) + (t1.z - t2.z )*(t1.z - t2.z ) );
return l;
}
/**指定の長さに縮小*/
public ThreeDimension setLen( ThreeDimension t1 , double m ){
double tl = this.getLen(t1);
if(tl==0.){ return t1; }
ThreeDimension rt = new ThreeDimension();
rt.x = t1.x * m/tl;
rt.y = t1.y * m/tl;
rt.z = t1.z * m/tl;
return rt;
}
/**開始点から終了点の距離の割合wだけ進んだ位置の点を返す*/
public ThreeDimension getWariaiPoint( ThreeDimension std , ThreeDimension endd , double w ){
ThreeDimension rd = this.plus( this.kakeru( this.minus(endd, std),w ) ,std );
return rd;
}
}
最終更新日: 2017-08-06 18:35:10